بغض بنود الفيزياء

من ويكي كتب

دليل دراسة الفيزياء/الحركة 
 دليل دراسة الفيزياء
• فهرس الكتاب
• القسم الأول | الحركة | القوى | الجاذبية | الزخم | العزم | الإحتكاك | العمل | الطاقة
• القسم الثاني | الدوران | الإهتزاز | الموجات | الصوت
• القسم الثالث | السوائل والغازات | حرارة | كهرومغنطيسية | إلكترونيات | بصريات
• الملاحق | وحدات | ثوابت | حروف إغريقية | كميات قياسية ومتجهات
محتويات
1 علم الحركة
2 الحركة الخطية
2.1 التنقل
2.2 السرعة
3 معادلات الحركة الخطية فے بعد واحد
4 الحركة الدورانية
4.1 الموقع الزاوي
4.2 السرعة الزاوية
4.3 التسارع الزاوي
4.4 العلاقة بين الكميات الدورانية والخطّية
4.4.1 التنقـل
4.4.2 السـرعة الخطّية
5 الحركة في أكثر من بعد
علم الحركة

 للمزيد من التفاصيل طالع مقالة ويكيبيديا: علم الحركة.

علم الحركة (Kinematics) هو فرع من فروع الميكانيكا (Mechanics) يصف حركة الأجسام والنظم المادية. هناك مفهومان أساسيان لصياغة نظريات علم الحركة بشكلها الكلاسيكي، وهما ثبات الأبعاد المكانية وإسقلاليتها عن الزمن. نستطيع وصف حركة جسم مادي نقطي في فضاء إقليدي باستخدام ثلاثة مفاهيم وهي التنقل، والسرعة والتسارع. بالنسبة للأجسام الحقيقية (التي لا يمكن وصفها بكونها نقاطا رياضاتية)، يصف علم الحركة تنقل ودوران مركز الكتلة (Center of mass) الجسم في فضاء ثلاثي الأبعاد. حاليا سنركز على الحركة الخطية المنتظمة، ثم في وقت لاحق على الحركة الدائرية.
الحركة الخطية

يعرف التنقل، والسرعة والتسارع على النحو التالي.
التنقل

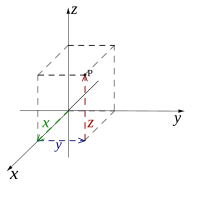
ص. 1- موقع جسم (P) في فضاء ثلاثي الأبعاد.

ص. 2- تمثيل موقع جسم على محور يمثل بعداً واحداً.

عندما نبحث عن تنقل جسم نسأل هذه الأسئلة "هل غير الجسم موقعه ؟ في أي اتجاه ؟". أول شيء يجب فعله هو تثبيت نقطة مرجعية لدراسة التنقل. يوصف موقع الجسم في الفضاء بإحداثياته الثلاثة (x, y, z) في إطار نظام إحداثي ديكارتي (Cartesian coordinate system) (ص. 1). باستعمال الإحداثيات الديكارتية تكتب متجهة (Vector) التنقل من الأصل إلى نقطة ( x , y , z ) {\displaystyle (x,y,z)} : r → = x ı ^ + y ȷ ^ + z k ^ {\displaystyle {\vec {r}}=x{\hat {\imath }}+y{\hat {\jmath }}+z{\hat {k}}}

أو r → ( x y z ) {\displaystyle {\vec {r}}{\begin{pmatrix}x\\y\\z\end{pmatrix}}} ( ı ^ , ȷ ^ , k ^ ) {\displaystyle ({\hat {\imath }},{\hat {\jmath }},{\hat {k}})} هي متجهات الوحدة في نظام الإحداثيات الديكارتية.

عندما تتم الحركة في بعد واحد (ص. 2) لنقل على سبيل المثال (x) فإن التنقل هو متجهة، يمكن حسابها كالآتي :
(1.1) Δ x → = x → f − x → i = ( x f − x i ) ı ^ {\displaystyle \Delta {\vec {x}}={\vec {x}}_{f}-{\vec {x}}_{i}\,=(x_{f}-x_{i})\,{\hat {\imath }}}


أي أنه الفرق بين الموقع (ونرمز له بالحرف الإغريقي Δ {\displaystyle \Delta } ) الذي كان فيه الجسم في النهاية ( x f {\displaystyle x_{f}\,} ) وموقعه عند البداية ( x i {\displaystyle x_{i}\,} ).

في علم الحركة هناك فرق بين "المسافة" (Distance) و"التنقل" (Displacement)، تخيل أن جسما ما يدور حول مركز؛ المسافة التي يقطعها عندما ينهي دورته هي بكل بساطة محيط الدائرة، ولكن التنقل هو صفر لأنه رجع لنقطة البداية.
السرعة

في علم الحركة، هناك فرق بين "السرعة (Speed)" و"السرعة الاتجاهية (Velocity)". فأما الأولى فهي كمية قياسية (Scalar) وأما الثانية فهي كمية إتجاهية (Vector).

توصف السرعة الاتجاهية المتوسطة (Average velocity) في بعد واحد بأنها نتاج قسمة كمية اتجاهية وهي التنقل، بكمية قياسية وهي المدة الزمنية التي يستغرقها التنقل:
(1.2) ⟨ v → ⟩ = Δ x → Δ t {\displaystyle \langle {\vec {v}}\rangle ={\frac {\Delta {\vec {x}}}{\Delta t}}}


وتعرف السرعة الاتجاهية اللحظية (Instantaneous velocity)، حسب حساب التفاضل، على أنها إشتقاق التنقل بالنسبة للزمن:
(1.3) v → = d x → d t {\displaystyle {\vec {v}}={\frac {\mathrm {d} {\vec {x}}}{\mathrm {d} t}}}


الحرف (d) يعني التنقل الذي يطرأ في فترة متناهية الصغر من الزمن، وهي اختصار للعبارة التالية: d x → d t = lim t → 0 Δ x → Δ t {\displaystyle {\frac {\mathrm {d} {\vec {x}}}{\mathrm {d} t}}=\lim _{t\to 0}{\frac {\Delta {\vec {x}}}{\Delta t}}}

السرعة الاتجاهية اللحظية يمكن أن تكون موجبة أو سالبة أو صفرا ووحدتها هي متر \ ثانية (m/s). اما (instantaneuos speed =مطلقInstantaneous velocity

نص عنص عريضريض=== التسارع === "هل يغير الجسم سرعته ؟" يجيب عن هذا التساؤل البحث عن التسارع (Acceleration) أو العجلة.

يعرف التسارع المتوسط، وهو كمية اتجاهية، على أنه معدل تغير السرعة في فترة من الزمن:
(1.4) ⟨ a → ⟩ = v f → − v i → t f − t i = Δ v → Δ t {\displaystyle \langle {\vec {a}}\rangle ={\frac {{\vec {v_{f}}}-{\vec {v_{i}}}}{t_{f}-t_{i}}}={\frac {\Delta {\vec {v}}}{\Delta t}}}


والتسارع اللحظي هو اشتقاق السرعة الاتجاهية اللحظية بالنسبة للزمن، أي أنه المشتقة الثانية للتنقل:
(1.5) a → = d v → d t = d 2 x → d t 2 {\displaystyle {\vec {a}}={\frac {\mathrm {d} {\vec {v}}}{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}{\vec {x}}}{\mathrm {d} t^{2}}}}


التسارع اللحظي هو كمية اتجاهية يمكن أن يكون:

• موجباً وهذا يعني أن سرعة الجسم تتصاعد (يعجل).

• سالباً وهذا يعني أن الجسم يبطئ.

• صفراً وهذا يعني أن الجسم إما ساكن أو يسير بحركة منتظمة دون تسارع أو تباطؤ.

وحدة التسارع هي متر \ مربع ثانية (m/s2).

هناك من يستعمل أيضا، خاصة في الملاحة الفضائية، المشتقة الثانية للسرعة وهو ما يعبر عنه بالـزخّة أو التسارع المركب (jerk):
(1.6) j → = d a → d t = d 2 v → d t 2 = d 3 x → d t 3 {\displaystyle {\vec {j}}={\frac {\mathrm {d} {\vec {a}}}{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}{\vec {v}}}{\mathrm {d} t^{2}}}={\frac {\mathrm {d} ^{3}{\vec {x}}}{\mathrm {d} t^{3}}}}

 
وحدة الـزخّة هي متر \ مكعب ثانية (m/s3).
معادلات الحركة الخطية فے بعد واحد

عندما يسير الجسم بتسارع منتظم، وهذا يعني أن سرعته تزيد بنفس القيمة في فترات متساوية من الزمن، فهذا يعني حسب (مـ 1.6) أن: j → = d a → d t = 0 {\displaystyle {\vec {j}}={\frac {\mathrm {d} {\vec {a}}}{\mathrm {d} t}}=0}

وهذا ما يحدث مثلاً مع السقوط الحرّ للأجسام في حقل الجاذبية الأرضية، فالتسارع ذو قيمة ثابتة. عندما ينطلق جسم في هذه مثل هذه الضروف بسرعة بقيمة سرعة بدائية ( u {\displaystyle u\,} ) لينتهي إلى موقع ما في زمن ( t {\displaystyle t\,} )، فإن قيمة سرعته النهائية ( v {\displaystyle v\,} ) هي:
(1.7) v = u + a t {\displaystyle v=u+at\,}


وبما أن التنقل الذي يحدث في بعد واحد ( s {\displaystyle s\,} ) بين هاذين الموقعين هو تكامل السرعة، سنتحصل على:
(1.8) s = s 0 + u t + 1 2 a t 2 {\displaystyle s=s_{0}+ut+{\begin{matrix}{\frac {1}{2}}\end{matrix}}{at^{2}}}


هنا ( s 0 {\displaystyle s_{0}\,} ) هو موقع الجسم عند البداية.

الآن بدمج (مـ 1.7) و(مـ 1.8) ننتهي إلى المعادلة الثالثة للحركة وهي:
(1.9) v 2 = u 2 + 2 a ( s − s 0 ) {\displaystyle v^{2}=u^{2}+2a(s-s_{0})\,}


أو حسب (1.1) على هذا الشكل: v 2 = u 2 + 2 a Δ s {\displaystyle v^{2}=u^{2}+2a\Delta s\,}

هذه المعادلة مفيدة جداً لحساب السرعة عندما لا نمتلك معلومات عن الأوقات.
الحركة الدورانية

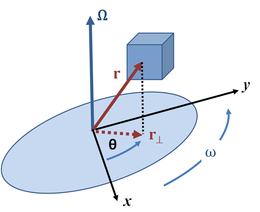
ص. 3- وصف الحركة الدائرية.

حركة الدوران هي حركة تتم في بعدين على مسار دائري يسمى مداراً. يمكن أن تكون الحركة منتظمة أي أن السرعة الزاوية ثابتة، أو غير منتظمة عندما تتغير السرعة حسب الزمن. يمكن أن يدور الجسم حسب محاور عديدة ولكننا سنختار هنا الحالة التي يدور فيها حول المحور (z).
الموقع الزاوي

المسافة المتجهة من مركز المدار، المنتمي لمحور الدوران، إلى نقطة ما في الجسم الدائر هي متجهة التنقل التي تحدد موقع الجسم ( r → {\displaystyle {\vec {r}}} ) في كل لحظة من الزمن (ص. 3). هناك إسقاط لهذه المتجهة على المستوي المعامد لمحور المدار نرمز له ب( r → ⊥ {\displaystyle {\vec {r}}_{\perp }} ). الزوية ( θ {\displaystyle \theta } ) التي تكونها هذه المكونة العمودية مع المحور (x) هي حسب الاتفاق الموقع الزاوي للجسم الدائر. اصطلاحاً، إذا كان الجسم يتحرك في الاتجاه المخالف لعقارب الساعة فإن الموقع الزاوي يكون موجباً والعكس بالعكس.

وحدة قياس الموقع الزاوي هي الراديان (Radian) إختصاراً (rad).
السرعة الزاوية

المعدل الذي يتغير به الموقع الزاوي حسب الزمن يعرف على أنه السرعة الزاوية ( ω {\displaystyle \omega } ). وتكتب قيمة السرعة الزاوية اللحظية كالآتي:
(1.9) ω = d θ d t {\displaystyle \mathbf {\omega } ={\frac {\mathrm {d} \theta }{\mathrm {d} t}}}


تمثل السرعة الزاوية بمتجهة ( Ω → {\displaystyle {\vec {\Omega }}} ) مطابقة لمحور الدوران حيث تكون قيمتها ( ω {\displaystyle \omega } )، وإتجاهها محدداً بإتجاه الدوران (إلى الأعلى إذا كان الدوران يتم عكس إتجاه عقارب الساعة وإلى أسفل إذا كان الدوران يتم في نفس إتجاه عقارب الساعة).

وحدة قياس السرعة الزاوية هي الراديان \ ثانية (rad/s).
التسارع الزاوي

قيمة التسارع الزاوي ( α {\displaystyle \alpha } ) هي معدل تغير قيمة السرعة الزاوية بالنسبة للزمن:
(1.10) α = d ω d t {\displaystyle \mathbf {\alpha } ={\frac {\mathrm {d} \mathbf {\omega } }{\mathrm {d} t}}}


وحدة قياس التسارع الزاوي هي الراديان \ مربع ثانية ( r a d / s 2 {\displaystyle \mathrm {rad/s^{2}} } ).
العلاقة بين الكميات الدورانية والخطّية

ص. 4- وصف حركة دائرية بنظام الإحداثيات القطبية.
التنقـل

يحدد تنقل جسم دائر بمتجهة قيماتها اللحظية هي:
(1.11) r → ( t ) = R u ^ R ( t ) {\displaystyle {\vec {r}}(t)=R\,{\boldsymbol {\hat {u}}}_{R}(t)\ }


حيث ( u ^ R {\displaystyle {\boldsymbol {\hat {u}}}_{R}} ) هي متجهة وحدة تشير إلى الخارج، من محور الدوران إلى الجسم الدائر. و ( R {\displaystyle R} ) هو نصف قطر المدار.
السـرعة الخطّية

السرعة الخطية لجسم دائر ( v → {\displaystyle {\vec {v}}\,} ) هي حسب (1.3) تفاضل التنقل بالنسبة للزمن: v → ( t ) = d d t r → ( t ) = d R d t u ^ R + R d u ^ R d t {\displaystyle {\vec {v}}(t)={\frac {\mathrm {d} }{\mathrm {d} t}}{\vec {r}}(t)={\frac {\mathrm {d} R}{\mathrm {d} t}}{\boldsymbol {\hat {u}}}_{R}+R{\frac {\mathrm {d} {\boldsymbol {\hat {u}}}_{R}}{\mathrm {d} t}}\ }

إذا إعتبرنا أن نصف قطر المدار ( R {\displaystyle R\,} ) ثابت طيلة الوقت، فإن المكونة الشعاعية للسرعة ( v → ⊥ {\displaystyle {\vec {v}}_{\perp }} ) هي صفر. وبما أن ( u ^ R {\displaystyle {\boldsymbol {\hat {u}}}_{R}} ) هي متجهة وحدة ذات قيمة ثابتة فإن تغيرها مع الوقت لا يمكن أن يكون سوى نتيجة دوران هذه الأخيرة على منوال متجهة التنقل ( r → {\displaystyle {\vec {r}}} ) التي تشير دائما نحو الجسم الدائر (أنظر ص. 4). وهذا يعني أن ( u ^ R {\displaystyle {\boldsymbol {\hat {u}}}_{R}} ) ترسم قوساً ( d θ {\displaystyle \mathrm {d} \theta } ) في مقدار من الزمن ( d t {\displaystyle \mathrm {d} t} )، أو بعبارة أخرى: d u ^ R d t = d θ d t u ^ θ {\displaystyle {\frac {\mathrm {d} {\boldsymbol {\hat {u}}}_{R}}{\mathrm {d} t}}={\frac {\mathrm {d} \theta }{\mathrm {d} t}}{\boldsymbol {\hat {u}}}_{\theta }\ }

حيث أن ( u ^ θ {\displaystyle {\boldsymbol {\hat {u}}}_{\theta }} ) هي متجهة وحدة معامدة ل( u ^ R {\displaystyle {\boldsymbol {\hat {u}}}_{R}} ) وهي تشير بذلك إلى إتجاه الحركة. وبما أن الجسم يتحرك بسرعة لحظية زاوية مقدارها ( ω {\displaystyle \omega } )، إذن فالتغير في متجهة الوحدة ( u ^ R {\displaystyle {\boldsymbol {\hat {u}}}_{R}} ) هي نتيجة الجداء الاتجاهي (Cross product) (×) لهذه الأخيرة مع متجهة السرعة الزاوية ( Ω → {\displaystyle {\vec {\Omega }}} ): d d t u ^ R ( t ) = Ω → × u ^ R = ω ( t ) u ^ θ {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}{\boldsymbol {\hat {u}}}_{R}(t)={\vec {\Omega }}\mathbf {\times {\boldsymbol {\hat {u}}}} _{R}=\omega (t)\mathbf {\boldsymbol {\hat {u}}} _{\theta }\ }

إذن السرعة الخطية في كل لحظة هي:
(1.12) v → ( t ) = R ω ( t ) u ^ θ {\displaystyle {\vec {v}}(t)=R\,\omega (t){\boldsymbol {\hat {u}}}_{\theta }\ }


أو بصيغة أكثر بساطة وذلك بإعتبار الكميات القياسية فقط: v = R ω {\displaystyle v=R\,\omega }
الحركة في أكثر من بعد


يقال أن الحركة ثنائية الأبعاد إذا ما كانت تتم في مستوي، وثلاثية الأبعاد إذا ما كانت تتم في الفضاء.



======



محتويات
1 تعريف القوة
2 قانون نيوتن الأول للحركة = مبدأ القصور الذاتي
3 قانون نيوتن الثاني للحركة = مبدأ الديناميكا
4 قانون نيوتن الثالث للحركة = مبدأ الفعل ورد الفعل
تعريف القوة


محصل مجموع القوى التي تسلط على جسم تتسبب في تسارعه. مقدار هذا التسارع يرجع إلى القصور الذاتي للجسم(أي مقاومة الجسم للتغير الذي يطرء في حركته) والذي يقاس عن طريق الكتلة. عندما قام إسحاق نيوتن بصياغة مبادأ الميكانيكا الكلاسيكية، إكتشف ثلاثة قوانين أساسية للحركة.
قانون نيوتن الأول للحركة = مبدأ القصور الذاتي




قانون نيوتن الثاني للحركة = مبدأ الديناميكا
قانون نيوتن الثالث للحركة = مبدأ الفعل ورد الفعل


========


/الجاذبية

< دليل دراسة الفيزياءاذهب إلى التنقلاذهب إلى البحث



دليل دراسة الفيزياء
• فهرس الكتاب (تعديل)
• القسم الأول | الحركة | القوى | الجاذبية | الزخم | العزم | الإحتكاك | العمل | الطاقة
• القسم الثاني | الدوران | الإهتزاز | الموجات | الصوت
• القسم الثالث | السوائل والغازات | حرارة | كهرومغنطيسية | إلكترونيات | بصريات
• الملاحق | وحدات | ثوابت | حروف إغريقية | كميات قياسية ومتجهات


قوة الجاذبية تبقي الكواكب في المجموعة الشمسية ضمن مدار معين

الجاذبية أو الثقالة (Gravity) هي ميل الكتل والأجسام للتحرك والانجذاب نحو بعضها البعض كما في الجاذبية بين الأرض والشمس.

فالوزن هو القوة التي تحثها الجاذبية محدثة الانجذاب بين الأرض والجسم المعني وهي تساوي جداء تسارع الجاذبية في كتلة الجسم. وكان أول من وضع نظرية للجاذبية هو الفبزبائي المعروف أسحاق نيوتن وبقيت هذه النظرية صامدة حتى تم استبدالها من قبل آينشتاين بنظرية النسبية العامة لكن معادلة نيوتن تبقى صحيحة وأكثر عملية عندما نتحدث عن حقول جاذبية ضعيفة كإرسال المركبات الفضائية والتطبيقات الهندسية الانشائية مثل بناء الجسور المعلقة.

انتشر مصطلح الجاذبية الأرضية مبكرا كون فكرة التجاذب كانت راسخة حسب النظرة النيوتنية، لاحقاً انتشر مصطلحي الجاذبية كتعميم لظاهرة التجاذب بين أي جسمين، ومصطلح ثقالة المشتق من الثقل وهو أكثر دلالة على مفهوم النظرية النسبية للثقالة حيث تعتبر النسبية الثقالة أو الجاذبية مجرد التواء في الزمكان وليس هناك من أي تجاذب بين الأجسام. بشكل عام قد يكون من الأنسب استخدام مصطلح "جاذبية" في إطار الميكانيكا الكلاسيكية في حين يستخدم مصطلح "ثقالة" في إطار النظرية النسبية.


محتويات

1 الجاذبية في الميكانيكا الكلاسيكية
2 حقل الجاذبية
3 طبيعة قوى الجاذبية حسب النظريات الفيزيائية
4 تاريخ نظرية الجاذبية
4.1 الثورة العلمية
4.2 دور العرب
4.3 قانون نيوتن للثقالة
4.4 نظرية النسبية
الجاذبية في الميكانيكا الكلاسيكية

قانون الجذب العام لنيوتن هو قانون استنباطي كمحاولة لوصف قوى الجاذبية بين الأجسام غير المشحونة، وقد استنبطه نيوتن من خلال مشاهدات فلكية عديدة وبالاستعانة بقوانين كيبلر لحركة الكواكب. كان البيروني والخازني أيضاً قد أشارا لهذا المفهوم قبلهما بسبعة قرون تقريباً.

يقول قانون الجاذبية العام لنيوتن : أن كل جسم يجذب جسما آخر في الكون بقوة محمولة على الخط الواصل بين المركزين وشدتها متناسبة طرديًا مع كتلتيهما وعكسيًا مع مربع المسافة بينهما.

الصورة القياسية لقانون الجذب العام لنيوتن F = G m 1 m 2 r 2 {\displaystyle F=G{\frac {m_{1}m_{2}}{r^{2}}}}

حيث: F {\displaystyle F\ } هي القوة الناتجة عن الجاذبية G {\displaystyle G\ } هو ثابت الجذب العام بين الكتل m 1 {\displaystyle m_{1}\ } هي كتلة الجسيم الأول m 2 {\displaystyle m_{2}\ } هي كتلة الجسيم الثاني r {\displaystyle r\ } هو البعد بين الجسيمين
الصورة متجه|الاتجاهية لقانون الجذب العام لنيوتن F → 12 = − F → 21 = − G m 1 m 2 | r → 12 | 2 r ^ 12 {\displaystyle {\vec {F}}_{12}=-{\vec {F}}_{21}=-G{m_{1}m_{2} \over {\vert {\vec {r}}_{12}\vert }^{2}}\,{\hat {r}}_{12}}

حيث: F → 12 {\displaystyle {\vec {F}}_{12}} هو متجه القوة التي يؤثر بها الجسيم 1 على الجسيم 2 F → 21 {\displaystyle {\vec {F}}_{21}} هو متجه القوة التي يؤثر بها الجسيم 2 على الجسيم 1 G {\displaystyle G\ } هو ثابت الجذب العام بين الكتل m 1 {\displaystyle m_{1}\ } و m 2 {\displaystyle m_{2}\ } هما كتلتا الجسيمين على الترتيب | r → 12 | = | r → 2 − r → 1 | {\displaystyle \vert {\vec {r}}_{12}\vert \ =\vert {\vec {r}}_{2}-{\vec {r}}_{1}\vert } هو البعد بين الجسيمين (أي مقدار المتجه الذي هو مقدار الفرق بين متجهي موضع الجسيمين) r ^ 12 = d e f r → 2 − r → 1 | r → 2 − r → 1 | {\displaystyle {\hat {r}}_{12}\ {\stackrel {\mathrm {def} }{=}}\ {\frac {{\vec {r}}_{2}-{\vec {r}}_{1}}{\vert {\vec {r}}_{2}-{\vec {r}}_{1}\vert }}} هو وحدة متجه للمتجه من 1 إلى 2

هذا القانون مثل معظم قوانين الميكانيكا الكلاسيكية يطبق على الاجسام النقطية الجسيمات أما الأجسام الكبيرة ذات الاشكال المختلفة فنعمد إلى تطبيق حسبان التكامل من أجل الحصول على شدة قوة الجاذبية المطبقة عليها.

ويمكن ملاحظة أن الصورة الاتجاهية لقانون الجذب العام لنيوتن هي نفس الصورة القياسية ، إلا أن F الآن كمية متجهة ، ويتم ضرب الجانب الأيمن بمتجه الوحدة المناسب .
حقل الجاذبية

حقل الجاذبية هو حقل متجه الذي يصف قوة الجاذبية التي سيتم تطبيقها على أي كائن في نقطة معينة في الفضاء ، لكل وحدة الكتلة. هو في الواقع يساوي تسارع الجاذبية عند تلك النقطة. وهو تعميم لنموذج المتجه، الذي يصبح مفيدا بشكل خاص إذا تم إشراك أكثر من كائنين (مثل صاروخ بين الأرض والقمر). بالنسبة لكائنين (مثل object 2 صاروخ، و object 1 الأرض) ، سنكتب r بدلا من r12 وm بدلا من m2 وبالتالي يمكن تحديد حقل الجاذبية g(r) على النحو التالي : g ( r ) = − G m 1 | r | 2 r ^ {\displaystyle g(r)=-G{\frac {m_{1}}{{\vert \ r\vert }^{2}}}{\hat {r}}}

وبالتالي يمكن كتابة: F ( r ) = m g ( r ) {\displaystyle F(r)=mg(r)}
طبيعة قوى الجاذبية حسب النظريات الفيزيائية

تعتبر قوة الجاذبية في الميكانيكا الكلاسيكية قوة مباشرة بعيدة المدى بمعنى أن هذه القوة تستطيع التأثير عن بعد بدون واسطة ويتم تأثيرها بشكل لحظي فأي تغير في موقع أحد الجسمين يرافقه تحول لحظي في الجاذبية بينه وبين الجسم الآخر، ولكي يفسر اسحاق نيوتن هذه الخاصية عمد إلى تعريف حقل جاذبية كوني موجود في كل نقطة من الفضاء. هذا الحقل هو حقل اتجاهي يعبر عنه بمتجه في كل نقطة ويمثل قوة الجاذبية التي تتعرض لها وحدة الكتل عندما توضع في هذه النقطة.

تنص نظرية النسبية العامة لآينشتاين على أن وجود أي شكل من أشكال المادة أو الطاقة أو العزم يحدث انحناء في الزمكان، وبسبب هذا الانحناء فان المسارات التي تسلكها الأجسام في الأطر المرجعية القصورية يمكن أن تنحرف أو تغير اتجاهها ضمن الزمن. وهذا الانحراف يظهر لنا على أنه تسارع نحو الاجسام الكبيرة وعرفه نيوتن بأنه ثقالة أو جاذبية. وبالتالي فان النسبية العامة ترى تسارع الجاذبية أو السقوط الحر بأنه حركة قصورية فعليا (منتظمة) في حين أن المراقب هو من يتحرك حركة متسارعة، وهذا ما يعرف ب مبدأ التكافؤ.
تاريخ نظرية الجاذبية
الثورة العلمية

تشير الكتب التاريخية إلى أن العرب كانوا قد عرفوا عن الجاذبية وتأثيراتها إلا أن العمل على نظرية "الجاذبية الحديثة" في أواخر القرن السادس عشر وبداية القرن السابع عشر حيث قام غاليليو بتجربته الشهيرة التي رمى فيها كرات ذات كُتَل مختلفة من أعلى برج بيزا وبيّن ان سرعة وصول الجسم للأرض لا تتعلق بكتلته. لاحقاً قام أيضاً بتجربة دحرجة الكرات على سطح مائل واستنتج منها أن السبب الذي قد يؤدي إلى وصول الأجسام الأثقل للأرض قبل الأجسام الأخف في بعض الأحيان هو احتكاك الهواء في الغلاف الجوي بالجسم.
دور العرب

عرف العرب منذ القرن التاسع للميلاد قوة التثاقل الناشئة عن جذب الأرض للأجسام وأطلقوا عليها آنذاك اسم "القوة الطبيعية". كذلك أدرك علماء العرب و فلاسفتهم أن هذه القوة تتعاظم كلما كبر الجسم، كما في قول ابن سينا في القرن الرابع الهجري / العاشر الميلادي في كتابه (الإشارات والتنبيهات)

«القوة في الجسم الأكبر، إذا كانت مشابهة للقوة في الجسم الأصغر حتى لو فصل من الأكبر مثل الأصغر، تشابهت القوتان بالاطلاق، فانها في الجسم الأكبر أقوى وأكثر، إذ فيها من القوة شبيه تلك» – كتاب الإشارات والتنبيهات

و زيادة وقف علماء العرب و المسلمين تماماً الجاذبية الأرضية و يتضح ذلك جلياً في كتاباتهم ، منها ما جاء لسان أبي الريحان البيروني في كتابه (القانون المسعودي) حيث قال:

«الناس على الأرض منتصبوا القامات كاستقامة أقطار الكرة وعليها أيضاً تؤول الأثقال إلى أسفل»

ومنها ما جاء في كتابات الخازني حيث قال

«إن الأجسام الساقطة تنجذب نحو مركز الأرض و إن اختلاف قوة الجذب يرجع إلى المسافة بين الجسم الساقط و هذا المركز» – كتاب ميزان الحكمة وقال أيضا:

«الجسم الثقيل هو الذي يتحرك بقوة ذاتية أبداً إلى مركز العالم، أعني أن الثقل هو الذي له قوة الحركة إلى نقطة المركز» – كتاب ميزان الحكمة

كما شبّه الإدريسي جاذبية الأرض بجذب المغناطيس للحديد، لما قال في كتابه نزهة المشتاق في اختراق الآفاق:

«الأرض جاذبة لما في أبدانها من أثقال بمنزلة حجر المغناطيس الذي يجذب الحديد»

إلا أن اندثار علوم العرب والمسلمين بعد ذلك كانت لها أسباب عدة من أبرزها الشقاقات العربية وعدم تقبل بعض فقهاء الدين لهذه العلوم حتى أن منهم من قاموا بتكفير هؤلاء العلماء خاصة مع رفض كثير من هؤلاء العلماء لفكرة إدراج شؤون القرآن في هذه العلوم.
قانون نيوتن للثقالة

في سنة 1687 نشر عالم الفيزياء و الرياضيات الإنكليزي إسحاق نيوتن نظريته الشهيرة، وهي أن الأجسام تجذب بعضها البعض تبعاً لكتلتها ، وتعتمد قوة الجاذبية على مربع المسافة بين الجسمين المتجاذبين. وبكلماته: "استنتجت من هذا أن القوة التي تُبقي الكواكب في مساراتها متعلقة بتربيع البعد بين مركزيهما. من هنا قارنت القوة التي تمسك القمر في مساره بالقوى على سطح الأرض ووصلت إلى نتيجة قريبة جدا".
نظرية النسبية


في أوائل القرن العشرين وفي بحثين نُشر أولهما في عام 1905 وثانيهما في عام 1915، قام الفيزيائي الشهير ألبرت آينشتاين بتغيير مفهوم الجاذبية. فحسب نظرية نيوتن كانت الجاذبية هي قوة، بينما أثبتت النسبية أن الجاذبية هي مجال. فحسب النسبية ، الجاذبية هي عبارة عن انحناءات في الفراغ تُسببها الكتلة . فكلما كانت كتلة الجسم أكبر كلما انحناء الفضاء حوله أكبر . والأجسام الأقل كتلة سوف تقع في هذا الانحناء الذي صنعه الجسم الأول وبالتالي سيأسرها بجاذبيته. بهذا التفسير الجديد المدهش للجاذبية، وبدمج البعد الزماني الرابع بالأبعاد المكانية الثلاث، أصبحت النسبية واحدة من النظريتين الأكثر شهرة وأهمية في القرن العشرين مع نظرية الكم.

====


/الزخم


لقد تطرقنا إلى موضوع الحركة في الفيزياء وقلنا أن الحركة تنقسم إلى عدة أنواع منها وتطرقنا إلى الحركة المنتظمة بسرعة منتظمة وبخط مستقيم فالحركة المنتظمة بسرحة منتظمة هي الحركة التي تكون ثابتة في إاتجاه واحد...فلو طرأ تغيير على هذه الحرة فعلى سبيل المثال إذا كانت لدينا حركة دفعناها بقوة فسارت بسرعة ثابتة فإذا قمنا بزيادة القوة المؤثرة على الكرة في نفس الاتجاه أو في اتجاه معاكس ؟ نلاحظ تسارع الكرة بسرعة مقدارها (v2) إذا كانت القوة المؤثرة على الكرة في نفس اتجاه حركتها أو توقف الكره عن الحركة إذا كانت القوة في عكس اتجاه الحركة. فمن هذا المنطلق صاغ نيوتن قانونه الأول في الحركة الذي ينص على أن: [c]القانون الأول لنيوتن[/c]

(كل جسم يبقى على حالته السكونية أي السكون أو الحركة المنتظمة بسرعة ثابتة وبخط مستقيم مالم تؤثر عليه قوة أو مجموعة قوى تغير من هذه الحالة.)..... فهذا يعني أن الجسم يبقى ساكنا مالم تؤثر عليه قوة فتحركة أو يبقى متحركة بسرعة منتظمة وبخط مستقيم مالم تؤثر عليه قوة فتغير من سرعته أو من اتجاهه أو من كليهما معا.....

[c]قانون نيوتن الثاني[/c] قانون نيوتن الثاني يعتمد بدرجة أساسة على الممانعة التي يتعرض لها الجسم المتحرك إلتي تتسبب في اغيير سرعته وبالتالي التغير المستمر في التعجل إلى أن يتوقف الجسم عن الحركة..

فينص قانون نيوتن الثاني على: (إذا أثرت قوة(أو محصلة قوى) على جسم بحيث تكسبة سرعة فإن مقدار التسارع الذي يكسبه الجسم يتناسب طرديا مع القوة المؤثرة عليه)..... مثلا: إذا أثرت قوة على جسم مقدارها(F) كتلته (m) فإنها تكسبه تسارع مقداره (g) فمقدار القوة معطى بالعلاقة التالية:

[c]F=m * g[/c]

حيث أن: F:القوة بالنيوتن.

m: الكتلة بالكيلو جرام g: التعجيل الأرضي ومقادره غالبا معلوم وهو(9.8متر/ثانية^) (^ يعني الأس التربيعي).

أما قانون نيوتن الثالث فيتعلق بالفعل ورد الفعل حيث ينص على: ( لكل فعل رد فعل مساوي له في المقدار ومضاد له في الاتجاه).

أمثلة من الحياة اليومية لهذا القانون:

1- عند وضع ثقل على راحة يدك فان الثقل يؤثر بقوة ضغط إلى الأسفل ويكون رد الفعل لليد إلى أعلى لكي يساوي الفعل الواقع عليها.. 2- حركة القذيفة الصاروخية أو الصاروخ أو الرصاصة من البندقية حيث تكون حركة المواد النفاثة في عكس اتجاه المقذوف..... 3- الفرامل في السيارة.....

==


الطاقة

< دليل دراسة الفيزياءاذهب إلى التنقلاذهب إلى البحث


الطاقـة تُعرَّف في الفيزياء بأنها القدرة على أداء شغل. فمثلاً زيادة سرعة سيارة أو رفع حجر يتطلب شغلاً. وتقاس الطاقة والشغل بالوحدات نفسها. ويخلط الناس كثيرًا بين الطاقة والقدرة والقوة. فالقدرة هي معدّل بذل الشغل. والقوة هي الدفع أو الجذب المبذول على الجسم. وتؤدي القوة شغلاً طالما أنها تحرّك الجسم، ويمكن تعيين كمية الشغل بشدة القوة المستخدمة والمسافة التي يتحركها الجسم. والطاقة التي تقترِن بالحركة تُسمّى الطاقة الميكانيكية

أشكال الطاقة

الطفلة الموجودة على الأرجوحة توضح كيف تتحول الطاقة الكامنة إلى طاقة حركية وبالعكس. في الرسم إلى اليمين نرى أن الطفلة هي في وضع الحد الأقصى للطاقة الكامنة، ولكن دون طاقة حركية في الوضع (ب). وفي الرسم إلى اليسار فإن الجاذبية تؤرجحها إلى أسفل من الوضع (ب) وفي الوضع (ج) لا توجد للطفلة طاقة كامنة وإنما أقصى طاقة حركية هي التي تؤرجحها إلى النقطة (د). الطاقة إحدى المفاهيم الأساسية في الفيزياء، وكذلك الكتلة. وتوجد الطاقة في عِدّة أشكال. وكل شكل من أشكال الطاقة يمكن أن يتحوّل إلى آخر، في عملية تُسمّى تحوُّل الطاقة. فمثلاً الطاقة الحرارية التي نشعر بها قادمة من النار تصلنا في صورة إشعاع. والأجسام القريبة من النار تسخَنُ بوساطة الأشعة تحت الحمراء، وهي إحدى أشكال الأشعة الكهرومغنطيسية. وهذه الأجسام تكتسب الطاقة في شكل حرارة. والضوء أيضاً موجات كهرومغنطيسية، ولهذا فهو أحد أشكال الطاقة. وهناك أشكال أخرى من الطاقة مثل الطاقة الكيميائية والطاقة النووية والطاقة الكهربائية والكتلة.

والحياة الإنسانية كلُّها تعتمد على الطاقة التي نستقبلها من الشّمس على هيئة إشعاعات. فالأشعاعات الشمسية تحت الحمراء تدفئ الأرض وأشعتها الضوئية تعطي النبات الطاقة اللازمة لنموه. والنباتات تختزن الطاقة الشمسية في شكل طاقة كيميائية في عملية التركيب الضوئي والمواد الغذائية التي يكونها النبات هي الغذاء الذي تعتمد عليه جميع الكائنات الحية. وتستخدم الحيوانات والكائنات الحية الأخرى الطاقة الناتجة من الغذاء لدفع العمليات الجسمية وتحريك العضلات. وتختزن طاقة الشمس أيضاً في شكل طاقة كيميائية في الزيت والغازات والفحم الحجري. وقد نتجت هذه الأنواع من الوقود الأحفوري عن تآكل النباتات والكائنات الحية التي عاشت منذ ملايين السنين. ونحن نحرق هذا الوقود لاستخلاص الطاقة منه. ويحوّل الاحتراق الطاقة الكيميائية في الوقود إلى حرارة. والحرارة بالتالي يمكن أن تُحوَّل إلى طاقة ميكانيكية. فاحتراق الفحم الحجري مثلاً يمكن أن يُدير العنفات (التوربينات) البخارية التي تنتج الكهرباء في محطات توليد الطاقة الكهربائية. وفي هذه المحطات تتحول الطاقة الكيميائية في الفحم الحجري إلى طاقة حرارية تتحوّل بدورها إلى طاقة ميكانيكية. وتتحول الطاقة الميكانيكية في العنفات بوساطة المولدات إلى طاقة كهربائية.

والطاقة النووية شكل آخر من أشكال الطاقة، وتُختزن في نَوَى الذرات. وتنتج التفاعلات النووية، مثل الانشطار والاندماج طاقة في شكل حرارة وإشعاع. وتُنتج التفاعُلات الانشطارية الحرارة في المفاعلات النووية، وتولد التفاعلات الاندماجية حرارة شديدة في باطن الشمس. وفي الطبقات الخارجية للشمس تتحول الحرارة إلى الإشعاع الذي ينبعث من الشمس في كافة الاتجاهات، ونحن نستقبل جزءًا ضئيلاً فقط من هذا الإشعاع. وفي التفاعلات الانشطارية والاندماجية، تكون كتلة المواد الناتجة من التفاعل أقلّ بقليل من كتلتها قبل التفاعل، ولذا فإن جزءًا صغيراً من المادة يكون قد تحول إلى طاقة. وقد استنتج العلماء أنّ المادة والطاقة متكافئتان. وجميع العمليات محكومة بالتغيُّرات التي تحدث في الطاقة من شكل إلى آخر. الطاقة الكامنة والطاقة الحركية الطاقة الميكانيكية هي الطاقة الناتجة عن الحركة، أي بسبب تأثير القوة على الأجسام. والطاقة الحركية هي الطاقة التي يتمتع بها الجسم لأنه يتحرك. وتتناسب طاقة حركة الجسم طردياً مع كتلته ومربع سرعته. ولهذا، فإنّ للقطار الذي يتحرّك بسرعة 80 كم في الساعة طاقة تعادل أربعة أمثال طاقة قطار آخر يتحرّك بسرعة 40كم في الساعة. والقطار الساكن ليس له طاقة حركة. فكل طاقة الحركة التي اكتسبها أثناء حركته قد تحولت إلى حرارة، تولدت عن الاحتكاك في المكابح التي أوقفت القطار.

الطاقة الكامنة هي الطاقة الموجودة في الجسم بسبب وضعه أو حالته. وهي تمثل الشغل الذي بُذِل فعلاً، وتسمّى أحياناً الطاقة المختزنة. فإذا رفعنا صندوقاً من الأرض إلى منضدة، فإن طاقة وضع الجسم سوف تزداد بمقدار كمية الشغل اللازمة لرفعه إلى منضدة. ويمكن تحويل الطاقة الكامنة إلى أشكال أخرى من الطاقة. فإذا ما دفعنا الصندوق من فوق المنضدة فسوف يبدأ في السقوط وتتحول طاقته الكامنة إلى طاقة حركية. وعندما يصطدم الصندوق بالأرض يحدث اهتزازات على الأرض والهواء المحيط بها. وتسخن هذه الاهتزازات الأرض والهواء، وبهذا تكون الطاقة الحركية للجسم قد تحوّلت إلى طاقة حرارية.

الطاقة الكيميائية. أحد أشكال الطاقة الكامنة. فالجزيئات يمكن أن تخزّن الطاقة نتيجة لطاقة وضع الذرات التي تنشأ عن تأثير القوى بين الذرات في الجزيئات. وأثناء التفاعلات الكيميائية تأخذ الذرات في الجزيئات مواقع مختلفة، وتحدث تغيرات في الطاقات الكامنة لهذه الذرات. وإذا قلت الطاقة الكامنة فإن التفاعل ينتج طاقة تَظهر على شكل حرارة.

بقاء الطاقة

الإشعاع الشمسي يتحول إلى حرارة.

الطاقة الميكانيكية الناتجة عن دوران المراوح تتحول إلى طاقة كهربائية. لاحظنا أنّه خلال زمن سقوط الصندوق من المنضدة قلت طاقته الكامنة، بينما زادت طاقته الحركية. ولكن يظل مجموع الطاقتين ثابتاً أثناء السقوط. ويعبّر العلماء عن ذلك بقانون ينص على أنّ الطاقة تظلّ باقية. ولا ينطبق قانون بقاء الطاقة على حالة الصندوق الساقط فقط، ولكنه ينطبق على حالة الكون كلّه. وينص هذا القانون على أن الطاقة الكلية للكون ذات قيمة ثابتة دائمًا.

ويُمكن أن يُعدّ البندول مثالاً لكيفية تحوُّل الطاقة من شكل إلى آخر بينما تظلّ الطاقة الكلية ثابتة. فعندما يصل البندول إلى نهاية اهتزازاته تكون له طاقة حركية فقط. وتتحوّل هذه الطاقة إلى طاقة كامنة عندما يصل البندول مرة أخرى إلى أعلى نقطة في اهتزازاته.وسوف يستمر البندول في الاهتزاز طالما لا يوجد هناك احتكاك أو مقاومة من الهواء. ولكن الطاقة التي تستخدم في التغلب على مثل هذا الاحتكاك لا تُفقد، وإنما تتحول إلى حرارة، ونحن نعلم الآن أن المادة والطاقة ترتبطان ارتباطاً وثيقاً. ولذا فإن قانون بقاء الطاقة يشمل المادة أيضاً. فالطاقة لا تفنى ولا تأتي من العدم، ولكنها يمكن أن تنشأ من المادة وتتحوّل إليها. فهي مثلاً قد تتحول إلى مادة في معجّلات الجسيمات عند ظهور جُسيمات جديدة أثناء تصادم الجسيمات المعجَّلة عند سرعات فائقة. انظر : ط= ك ث2؛ الكتلة.

قياس الطاقة. تقاس الطاقة في النظام المتري بالجول. والجول الواحد هو كمية الشغل المبذول لتحريك جسم مسافة متر واحد ضد مقاومة قوة مقدارها نيوتن واحد. وتقاس الطاقة الكامنة للجاذبية بحاصل ضرب وزن الجسم في المسافة الرأسية التي يُمكن تحريكها أثناء سقوطه حتى يصل إلى حالة السُّكون. وتُقاس الطاقة الحركية بالعلاقة : الطاقة الحركية = ½ ك ع²، حيث ك هي كتلة الجسم، وع² هي مربع سرعته. والقدرة هي معدل أداء الشغل، ووحدتها الواط. وتساوي قدرة الآلة واط واحد إذا كانت تنتج جولا واحداً في كل ثانية.
تحيات اخوكم هيثم صلاح الدبعي الجابري 

================